Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

The equations that fall in love!

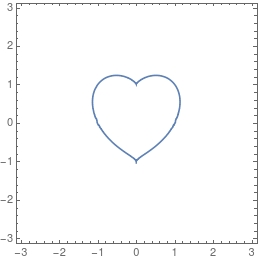lv The graph of the curve which looks like a heart : (x2+y2−1)3−x2y3=0

Probably you want to gift your loved one never ending and perpetual love. I will tell you what one could do. So obviously I wanted some thing however far you go from it you come back and fall in love ? so as a romantic I symbolize love by the symbol of a heart (How innovative!!)! That reduced my problem very much, so I need an oscillator which has a limit cycle which looks like a heart.

Hmm. You might say I know the function that looks like heart but how would you make a differential equation (so that things will move towards it) which has a limit cycle (a circley thing which attract nearby trajectories in strict mathematical terms :-) ) which looks the same ? So here is the simple answer : "co-ordinate transformation". You want your equations to be like love you better go to the world of love.

The method I am describing here is pretty general so you can create an oscillator that looks like a square, circle or anything circlish (A topological circle,) . What you need to do is the following.

Write down the equation that describe your favourite curve Remember the fact that ˙r=r(1−r) and ˙θ=1 has a limit cycle at r=1 Therefore, replace r by the equation of the favourite curve and θ by the ArcTan(x/y) Solve and get the differential equation.

An oscillator is a set of ODEs which gives oscillatory solutions (like a simple pendulum). A limit cycle is when for any 'nearby' point in phase space (space where x and y represent the states with no time axis) you come back to the same oscillating 'circle' in the phase space (not like a simple pendulum but like our solution here!)

So I did the same for heart equations. So what did I get? The answer is the following.

˙y=−(2(x12y+6x10y3−6x10y+15x8y5−2x8y4−30x8y3+15x8y+3x7+20x6y7−6x6y6−60x6y5+6x6y4+60x6y3−21x6y+9x5y2−6x5+15x4y9−6x4y8−59x4y7+12x4y6+90x4y5−6x4y4−63x4y3+18x4y+9x3y4−x3y3−12x3y2+3x3+6x2y11−2x2y10−30x2y9+6x2y8+60x2y7−6x2y6−63x2y5+3x2y4+36x2y3−9x2y+3xy6−xy5−6xy4+3xy2+y13−6y11+15y9−21y7+18y5−9y3+2y)/(6x6+18x4y2−12x4+18x2y4−5x2y3−24x2y2+6x2+6y6−12y4+6y2

and

˙x=−−3x2y22√(x2+y2−1)3−x2y3+3y(x2+y2−1)2√(x2+y2−1)3−x2y3+x(x2y3−(x2+y2−1)3+1)√(x2+y2−1)3−x2y3y2(x2y2+1)−x(3x(x2+y2−1)2√(x2+y2−1)3−x2y3−xy3√(x2+y2−1)3−x2y3)y2(x2y2+1)−3y(x2+y2−1)2√(x2+y2−1)3−x2y3−3x2y22√(x2+y2−1)3−x2y3y(x2y2+1)

And the beautiful solution of these equations is given below. Can you notice the love in the phase space and all the trajectories that fall towards it ?

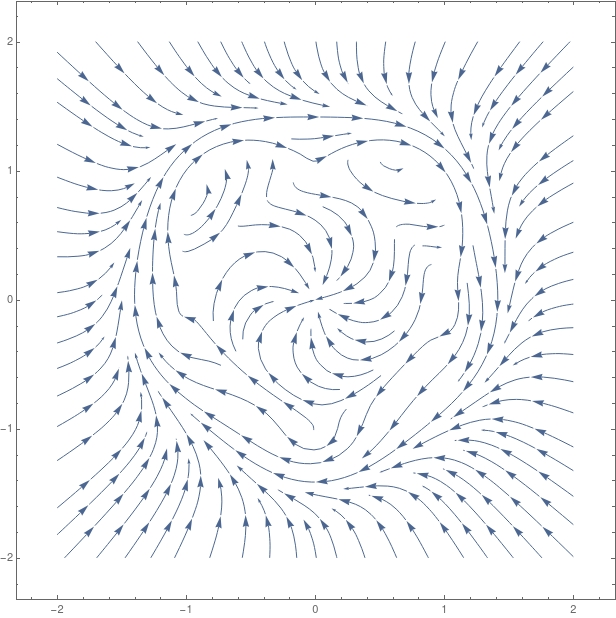lv_phase_space Solution of the horrible equations given above. Can you notice the love in the phase space? You start this equation at any initial conditions (away from the love) it will fall in love :).

Let's see what happens after you give this as a Christmas gift!! :-D :-D

Obtain a pdf version from here (Permanent DOI) :https://doi.org/10.5281/zenodo.1972823

Posts

subscribe via RSS