Newton's iteration as map - Part 1

Newton Iterations is a well known methodology to compute the solution of the problem f(x) = 0. It is very interesting to look at it as a map. The iteration step is as follows for x(n+1).

x(n+1)=x(n)−f(x(n))f′(x(n))

Let the function be Sin(x) then it results in the following map

x(n+1)=x(n)−tan(x(n))

The plot of the function and the line x=x is shown below. The points of the intersection of the line with x-Tan(x) function forms the solution of the newton iteration.

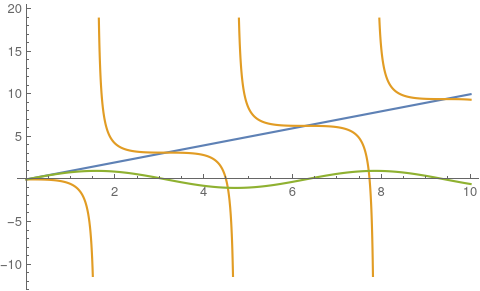
As you can see at the points where the sin(x) function change direction the map becomes very unstable. But in other areas it can converge to one solution depending on the initial condition.

To be continued . . .

Posts

subscribe via RSS